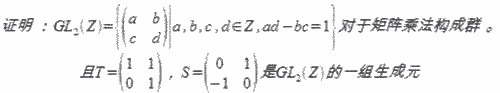你的阳光 学习频道

信息安全的数学基础

信息安全的数学基础 2007学年第二学期 陈恭亮老师作业题

2008-06-06交，共5题

  1. 2008-05-16课堂补充
    g2(x)=x+1是F28生成元，求g2(x)=x+1的定义多项式h(y)，判断h(y)是否为本原多项式
  2. 2008-05-16课堂补充
    求出F28的子域及其生成元，以及相应的定义多项式
  3. 2008-05-23课堂补充
    求F28=F2[x]/(x8+x4+x3+x2+1)的一个正规基
  4. 2008-05-28课堂补充
    F17上椭圆曲线E y2=x3+2x+5，求该椭圆曲线的全部点以及阶
  5. 2008-05-28课堂补充
    F17上椭圆曲线E y2=x3+2x-1，求该椭圆曲线的全部点以及阶

2008-05-16交，共8题

  1. 2008-05-04课堂补充
    求F2[x]中f(x)=x8+x4+x3+x+1的周期，并求y∈F2[x]/(f(x))，使得y、y2、y4、y8为F2[x]/(f(x))的基底
  2. 2008-05-04课堂补充
    求F2[x]中f(x)=x8+x4+x3+x2+1的周期，并求y∈F2[x]/(f(x))，使得y、y2、y4、y8为F2[x]/(f(x))的基底
  3. 2008-05-04课堂补充
    设a(x)=x3+x+1，b(x)=x2+x+1，计算a(x)+b(x)、a(x)．b(x)、a(x)/b(x)
  4. 第11章课件2
    证明：如果α≠0和β都是有理数域Q上的代数数，则α+β和α-1也是有理数域Q上的代数数
  5. 第11章课件3
    α叫做代数整数，如果存在一个首一正系数多项式f(x)，使得f(α)=0。证明：如果α≠0和β是代数整数，则α+β和α-1也是代数整数
  6. 第12章课件3
    证明x8+x4+x3+x+1是F2[x]中的不可约多项式，从而F2[x]/(x8+x4+x3+x+1)是一个F28域
  7. 第12章课件4
    求F28=F2[x]/(x8+x4+x3+x+1)中的生成元g(x)，并计算g(x)t，t=1,2,…,255和所有生成元
  8. 第12章课件3
    证明x8+x4+x3+x2+1是F2[x]中的不可约多项式，从而F2[x]/(x8+x4+x3+x2+1)是一个F28域

2008-05-04交，共3题

  1. 2008-04-18课堂补充
    求F2上的所有8次不可约多项式
    注：x8+x4+x3+x+1是不可约非本原多项式，用于AES；x8+x4+x3+x2+1是不可约本原多项式，用于欧洲通信标准
    提示：非零多项式有28-1=255个，次数为偶数时一定可约，奇数次系数为0时可约
  2. 2008-04-30课堂补充
    求Q(√2，3√3)的基底
  3. 2008-04-30课堂补充
    求u使Q(√2，√3)=Q(u)

2008-04-18交，共9题

  1. 对3DES对称密码算法的S盒进行轮换分解
    补充：DES算法标准FIPS 46-2 - (DES), Data Encryption Standard
    页面中搜索“PRIMITIVE FUNCTIONS FOR THE DATA ENCRYPTION ALGORITHM”就可找到标准建议的S盒函数
    还有一个C语言的3DES实现 FPGA芯片上的3DES实现思路
  2. 第十章课件14
    证明：置换群S4的一组生成元为(1,2),(1,3),(1,4)
    进一步，用该组生成元来给出S4的所有子群
  3. 第十章课件15
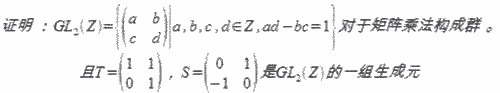
  4. 2008-04-11课堂补充
    假设K是有限域，p是K的特征。证明：p是奇数，且K的元素个数为pn
  5. 2008-04-11课堂补充
    设R是特征为p的交换环，证明：ψ:x→xp是R的一个自同态
  6. 2008-04-16课堂补充
    证明：若a/b=a'/b'，c/d=c'/d'，则必有(ad+bc)/bd=(a'd'+b'c')/b'd'以及ac/bd=a'c'/b'd'（不依赖代表元选择）
  7. 2008-04-16课堂补充
    证明课本10.3定理1
  8. 2008-04-16课堂补充
    证明：整数环是主理想环
  9. 2008-04-16课堂补充
    设(a)是Z的理想，(b)是Z的理想，证明(a,b)生成的理想是(gcd(a,b))

2008-03-21交，共2题

  1. 第九章课件10+上课补充
    分别求出(Z/31Z)*中的一个2阶元a、3阶元b、5阶元c，并计算ord(abc)，证明abc是生成元
  2. 第九章课件11
    求(Z/(31·43)Z)*中的所有元素的阶，并计算各阶的元素个数

2008-03-07交，共9题

  1. 第八章课件11
    证明F23的非零元对于乘法构成一个循环群，并求出其生成元
  2. 第八章课件12
    证明：Z/nZ中的可逆元对乘法构成一个群，记作Z/nZ*
  3. 第八章课件13
    证明：Z/26Z对乘法不构成一个群
  4. 第八章课件14
    构造26元的一个乘法群
  5. 2008-02-22课堂补充1
    证明：假设H是Z的真子群，则存在n，使得H=nZ
  6. 2008-02-22课堂补充2
    设群G，{Hi}i∈I是G的一族子群，则∪i∈IHi=H1∪H2∪…∪Hn∪…是否是G的子群？
    注：可以设G=Z(整数乘群或整数加群)，用Z的子群来表达
    答案：不是
  7. 第八章课件2
    证明：群G是交换群的充要条件是对任意a,b∈G，有(ab)2=a2b2
  8. 第八章课件7
    设a是群G的一个元素，证明：映射δ:x→axa-1是G到自身的自同构
  9. 第八章课件8
    设H是群G的子群。在G中定义关系R:aRb如果b-1a∈H。证明：
    ⑴R是等价关系
    ⑵aRb的充要条件是aH=bH